Real Numbers Definition Examples Properties Symbol Chart
1. Euclid’s Division lemma:- Given Positive integers a and b there exist unique integers q and r satisfying
a=bq +r, where 0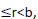 where a, b, q and r are respectively called as dividend, divisor, quotient and remainder.
where a, b, q and r are respectively called as dividend, divisor, quotient and remainder.
a=bq +r, where 0
2. Euclid’s division Algorithm:- To obtain the HCF of two positive integers say c and d, with c>0, follow the steps below:
Step I: Apply Euclid’s division lemma, to c and d, so we find whole numbers, q and r such that c =dq+r, 0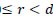
Step II: If r=0, d is the HCF of c and d. If r
Step III: Continue the process till the remainder is zero. The divisor at this stage will be the required HC
Step II: If r=0, d is the HCF of c and d. If r
Step III: Continue the process till the remainder is zero. The divisor at this stage will be the required HC
3. The Fundamental theorem of Arithmetic:-
Every composite number can be expressed ( factorised ) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.
Ex.: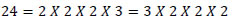
Every composite number can be expressed ( factorised ) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.
Ex.:
Theorem: LET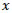 be a rational number whose decimal expansion terminates. Then
be a rational number whose decimal expansion terminates. Then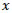 can be expressed in the form
can be expressed in the form


1. If the H C F of 657 and 963 is expressible in the form of 657x + 963x - 15 find x.Definition
(Ans:x=22)

(Ans:x=22)

2. Express the GCD of 48 and 18 as a linear combination. (Ans: Not unique)
 |
|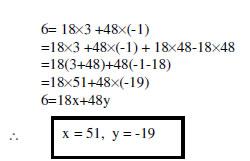
Hence, x and y are not unique.
3. Prove that one of every three consecutive integers is divisible by 3.
Ans:
n,n+1,n+2 be three consecutive positive integers
We know that n is of the form 3q, 3q +1, 3q + 2
So we have the following cases Properties
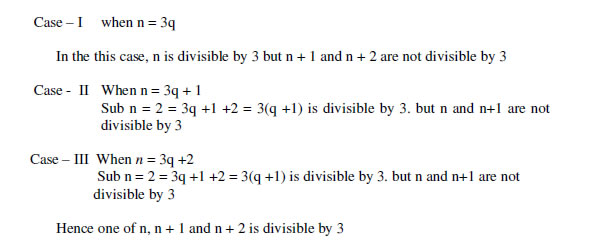
Ans:
n,n+1,n+2 be three consecutive positive integers
We know that n is of the form 3q, 3q +1, 3q + 2
So we have the following cases Properties
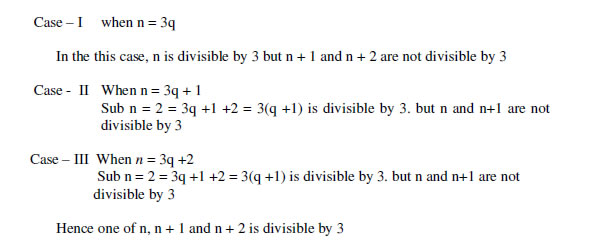
4. Find the largest possible positive integer that will divide 398, 436, and 542 leaving remainder 7, 11, 15 respectively.
(Ans: 17)
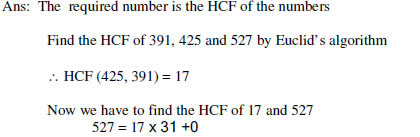

(Ans: 17)
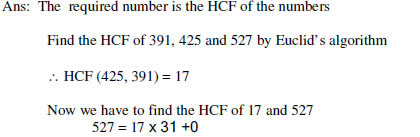
5. Find the least number that is divisible by all numbers between 1 and 10 (both inclusive).
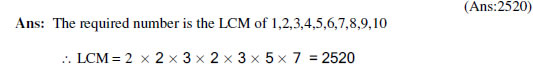
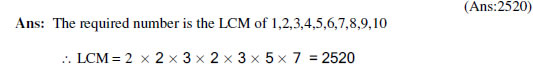
6. Show that 571 is a prime number.
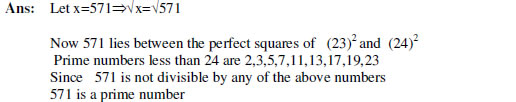
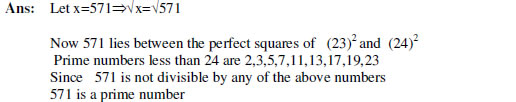
7. If d is the HCF of 30, 72, find the value of x & y satisfying d = 30x + 72y.

Hence, x and y are not unique

Hence, x and y are not unique
8. Show that the product of 3 consecutive positive integers is divisible by 6.
Ans: Proceed as in question sum no. 3
Ans: Proceed as in question sum no. 3
9. Show that for odd positive integer to be a perfect square, it should be of the form

11. If a and b are positive integers. Show that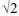 always lies between
always lies between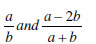
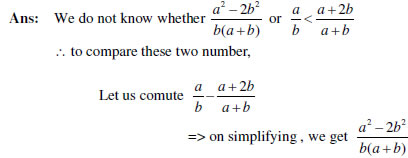
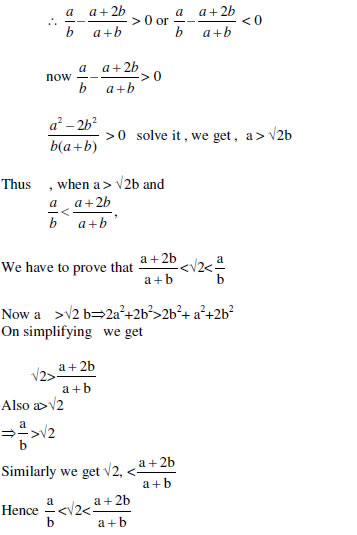
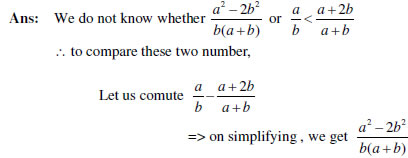
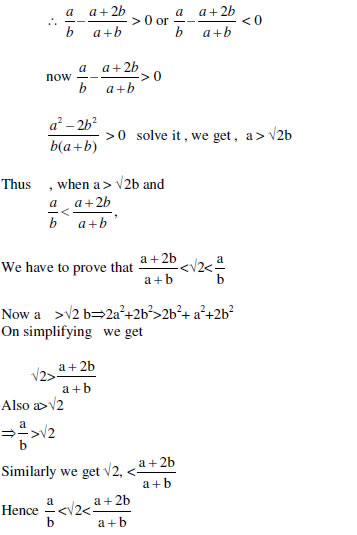
12. Prove that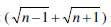 is irrational, for every n
is irrational, for every n N Symbol chart
N Symbol chart
More chapters for class 10 maths


إرسال تعليق