Complex numbers

Here we are going to discuss about complex numbers:

• What is complex number..?
• Calculations of complex numbers
• Addition of complex numbers
• Subtraction of complex numbers
• Multiplication of complex numbers
• What is iota(i) ..?
• What is the value of iota..?
• Theories of complex numbers..
• And many more..

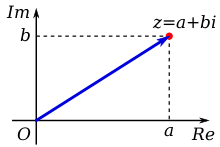
A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. "Re" is the real axis, "Im" is the imaginary axis, and i satisfies i² = −1.

A complex number is a number that can be expressed in the form a + bi, where a and bare real numbers, and i is a solution of the equation x² = −1. Because no real numbersatisfies this equation, i is called an imaginary number. For the complex number a + bi, a is called the real part, and b is called the imaginary part. Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers, and are fundamental in many aspects of the scientific description of the natural world.^{[note 1][1]}

Complex numbers allow solutions to certain equations that have no solutions in real numbers. For example, the equation

${\displaystyle (x+1)^{2}=-9}$

has no real solution, since the square of a real number cannot be negative. Complex numbers provide a solution to this problem. The idea is to extend the real numbers with an indeterminate i (sometimes called the imaginary unit) that is taken to satisfy the relation i² = −1, so that solutions to equations like the preceding one can be found. In this case the solutions are −1 + 3i and −1 − 3i, as can be verified using the fact that i² = −1:

${\displaystyle ((-1+3i)+1)^{2}=(3i)^{2}=\left(3^{2}\right)\left(i^{2}\right)=9(-1)=-9,}$

${\displaystyle ((-1-3i)+1)^{2}=(-3i)^{2}=(-3)^{2}\left(i^{2}\right)=9(-1)=-9.}$

According to the fundamental theorem of algebra, all polynomial equations with real or complex coefficients in a single variable have a solution in complex numbers. In contrast, some polynomial equations with real coefficients have no solution in real numbers. The 16th-century Italian mathematician Gerolamo Cardano is credited with introducing complex numbers in his attempts to find solutions to cubic equations.^[2]

Formally, the complex number system can be defined as the algebraic extension of the ordinary real numbers by an imaginary number i.^[3] This means that complex numbers can be added, subtracted, and multiplied, as polynomials in the variable i, with the rule i² = −1 imposed. Furthermore, complex numbers can also be divided by nonzero complex numbers. Overall, the complex number system is a field.

Geometrically, complex numbers extend the concept of the one-dimensional number lineto the two-dimensional complex plane by using the horizontal axis for the real part and the vertical axis for the imaginary part. The complex number a + bi can be identified with the point (a, b) in the complex plane. A complex number whose real part is zero is said to be purely imaginary; the points for these numbers lie on the vertical axis of the complex plane. A complex number whose imaginary part is zero can be viewed as a real number; its point lies on the horizontal axis of the complex plane. Complex numbers can also be represented in polar form, which associates each complex number with its distance from the origin (its magnitude) and with a particular angle known as the argumentof this complex number.

The geometric identification of the complex numbers with the complex plane, which is a Euclidean plane (${\displaystyle \mathbb {R} ^{2}}$), makes their structure as a real 2-dimensional vector space evident. Real and imaginary parts of a complex number may be taken as components of a vector with respect to the canonical standard basis. The addition of complex numbers is thus immediately depicted as the usual component-wise addition of vectors. However, the complex numbers allow for a richer algebraic structure, comprising additional operations, that are not necessarily available in a vector space; for example, the multiplication of two complex numbers always yields again a complex number, and should not be mistaken for the usual "products" involving vectors, like the scalar multiplication, the scalar product or other (sesqui)linear forms, available in many vector spaces; and the broadly exploited vector product exists only in an orientation-dependent form in three dimensions.

DefinitionEdit

An illustration of the complex plane. The real part of a complex number z = x + iy is x, and its imaginary part is y.

Based on the concept of real numbers, a complex number is a number of the form a + bi, where a and b are real numbers and i is an indeterminate satisfying i² = −1. For example, 2 + 3i is a complex number.^[4]

This way, a complex number is defined as a polynomial with real coefficients in the single indeterminate i, for which the relation i² + 1 = 0 is imposed. Based on this definition, complex numbers can be added and multiplied, using the addition and multiplication for polynomials. The relation i² + 1 = 0 induces the equalities i^4k = 1, i^4k+1 = i, i^4k+2 = −1, and i^4k+3 = −i,which hold for all integers k; these allow the reduction of any polynomial that results from the addition and multiplication of complex numbers to a linear polynomial in i, again of the form a + bi with real coefficients a, b.

The real number a is called the real part of the complex number a + bi; the real number b is called its imaginary part. To emphasize, the imaginary part does not include a factor i; that is, the imaginary part is b, not bi.^[5][6]

Formally, the complex numbers are defined as the quotient ring of the polynomial ring in the indeterminate i, by the ideal generated by the polynomial i² + 1 (see below).^[7]

NOTATION:

A real number a can be regarded as a complex number a + 0i whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi whose real part is zero. As with polynomials, it is common to write a for a + 0i and bi for 0 + bi. Moreover, when the imaginary part is negative, that is, b = −|b| < 0, it is common to write a − |b|iinstead of a + (−|b|)i; for example, for b = −4,3 − 4i can be written instead of 3 + (−4)i.

Since in polynomials with real coefficients the multiplication of the indeterminate i and a real is commutative, the polynomial a + bi may be written as a + ib. This is often expedient for imaginary parts denoted by expressions, for example, when b is a radical.^[8]

The real part of a complex number z is denoted by Re(z) or ℜ(z); the imaginary part of a complex number z is denoted by Im(z) or ℑ(z). For example,

${\displaystyle \operatorname {Re} (2+3i)=2\quad }$ and ${\displaystyle \quad \operatorname {Im} (2+3i)=3.}$

The set of all complex numbers is denoted by ${\displaystyle \mathbf {C} }$ (upright bold) or ${\displaystyle \mathbb {C} }$ (blackboard bold).

In some disciplines, in particular electromagnetism and electrical engineering, jis used instead of i since i is frequently used to represent electric current.^[9] In these cases complex numbers are written as a + bj or a + jb.

Main article: Complex plane

A complex number z, as a point (red) and its position vector (blue)

A complex number z can thus be identified with an ordered pair (Re(z), Im(z)) of real numbers, which in turn may be interpreted as coordinates of a point in a two-dimensional space. The most immediate space is the Euclidean plane with suitable coordinates, which is then called complex plane or Argand diagram,^[10][11] named after Jean-Robert Argand. Another prominent space on which the coordinates may be projected is the two-dimensional surface of a sphere, which is then called Riemann sphere.

Cartesian complex plane:

The definition of the complex numbers involving two arbitrary real values immediately suggest the use of Cartesian coordinates in the complex plane. The horizontal (real) axis is generally used to display the real part with increasing values to the right and the imaginary part marks the vertical (imaginary) axis, increasing values upwards.

A charted number may be either viewed as the coordinatized point, or as a position vector from the origin to this point. The coordinate values of a complex number z are said to give its Cartesian, rectangular, or algebraic form.

Notably, the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition, while multiplication (see below) corresponds to multiplying their magnitudes and adding the angles they make with the real axis. Viewed in this way the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin

${\displaystyle (a+bi)\cdot i=ai+b(i)^{2}=-b+ai.}$

Polar complex planeEdit

Main article: Polar coordinate system

"Polar form" redirects here. For the higher-dimensional analogue, see Polar decomposition.

Argument φ and modulus r locate a point in the complex plane.

Modulus and argument:

An alternative option for coordinates in the complex plane is the polar coordinate systemthat uses the distance of the point z from the origin (O), and the angle subtended between the positive real axis and the line segment Ozin a counterclockwise sense. This leads to the polar form of complex numbers.

The absolute value (or modulus or magnitude) of a complex number z = x + yi is^[12]

${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$

If z is a real number (that is, if y = 0), then r = |x|. That is, the absolute value of a real number equals its absolute value as a complex number.

By Pythagoras' theorem, the absolute value of complex number is the distance to the origin of the point representing the complex number in the complex plane.

The argument of z (in many applications referred to as the "phase" φ) is the angle of the radius Oz with the positive real axis, and is written as ${\displaystyle \arg(z)}$. As with the modulus, the argument can be found from the rectangular form ${\displaystyle x+yi}$^[13] by applying the inverse tangent to the quotient of imaginary-by-real parts. By using a half-angle identity a single branch of the arctan suffices to cover the range of the arg-function, (−π, π], and avoids a more subtle case-by-case analysis

${\displaystyle \varphi =\arg(x+yi)={\begin{cases}2\arctan \left({\dfrac {y}{{\sqrt {x^{2}+y^{2}}}+x}}\right)&{\text{if }}x>0{\text{ or }}y\neq 0,\\\pi &{\text{if }}x<0{\text{ and }}y=0,\\{\text{undefined}}&{\text{if }}x=0{\text{ and }}y=0.\end{cases}}}$

Normally, as given above, the principal valuein the interval (−π, π] is chosen. Values in the range [0, 2π) are obtained by adding 2π if the value is negative. The value of φ is expressed in radians in this article. It can increase by any integer multiple of 2π and still give the same angle, viewed as subtended by the rays of the positive real axis and from the origin through z. Hence, the arg function is sometimes considered as multivalued. The polar angle for the complex number 0 is indeterminate, but arbitrary choice of the polar angle 0 is common.

The value of φ equals the result of atan2:

${\displaystyle \varphi =\operatorname {atan2} \left(\operatorname {Im} (z),\operatorname {Re} (z)\right).}$

Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form

${\displaystyle z=r(\cos \varphi +i\sin \varphi ).}$

Using Euler's formula this can be written as

${\displaystyle z=re^{i\varphi }.}$

Using the cis function, this is sometimes abbreviated to

${\displaystyle z=r\operatorname {cis} \varphi .}$

In angle notation, often used in electronics to represent a phasor with amplitude r and phase φ, it is written as^[14]

${\displaystyle z=r\angle \varphi .}$

EqualityEdit

Two complex numbers are equal if and only ifboth their real and imaginary parts are equal. That is, complex numbers ${\displaystyle z_{1}}$ and ${\displaystyle z_{2}}$ are equal if and only if ${\displaystyle \operatorname {Re} (z_{1})=\operatorname {Re} (z_{2})}$ and ${\displaystyle \operatorname {Im} (z_{1})=\operatorname {Im} (z_{2})}$. Nonzero complex numbers written in polar form are equal if and only if they have the same magnitude and their arguments differ by an integer multiple of 2π.

OrderingEdit

Since complex numbers are naturally thought of as existing on a two-dimensional plane, there is no natural linear ordering on the set of complex numbers. In fact, there is no linear ordering on the complex numbers that is compatible with addition and multiplication – the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i² = −1.

ConjugateEdit

See also: Complex conjugate

Geometric representation of z and its conjugate ${\displaystyle {\overline {z}}}$ in the complex plane

The complex conjugate of the complex number z = x + yi is given by x − yi. It is denoted by either ${\displaystyle {\overline {z}}}$ or z*.^[24] This unary operation on complex numbers cannot be expressed by applying only their basic operations addition, subtraction, multiplication and division.

Geometrically, ${\displaystyle {\overline {z}}}$ is the "reflection" of z about the real axis. Conjugating twice gives the original complex number

${\displaystyle {\overline {\overline {z}}}=z,}$

which makes this operation an involution. The reflection leaves both the real part and the magnitude of ${\displaystyle z}$ unchanged, that is

${\displaystyle \operatorname {Re} ({\overline {z}})=\operatorname {Re} (z)\quad }$ and ${\displaystyle \quad |{\overline {z}}|=|z|.}$

The imaginary part and the argument of a complex number ${\displaystyle z}$ change their sign under conjugation

${\displaystyle \operatorname {Im} ({\overline {z}})=-\operatorname {Im} (z)\quad }$ and ${\displaystyle \quad \operatorname {arg} ({\overline {z}})\equiv -\operatorname {arg} (z){\pmod {2\pi }}.}$

For details on argument and magnitude, see the section on Polar form.

The product of a complex number ${\displaystyle z=x+yi}$ and its conjugate is always a positive real number and equals the square of the magnitude of each:

${\displaystyle z\cdot {\overline {z}}=x^{2}+y^{2}=|z|^{2}=|{\overline {z}}|^{2}.}$

This property can be used to convert a fraction with a complex denominator to an equivalent fraction with a real denominator by expanding both numerator and denominator of the fraction by the conjugate of the given denominator. This process is sometimes called "rationalization" of the denominator (although the denominator in the final expression might be an irrational real number), because it resembles the method to remove roots from simple expressions in a denominator.

The real and imaginary parts of a complex number z can be extracted using the conjugation:

${\displaystyle \operatorname {Re} (z)={\dfrac {z+{\overline {z}}}{2}},\quad }$ and ${\displaystyle \quad \operatorname {Im} (z)={\dfrac {z-{\overline {z}}}{2i}}.}$

Moreover, a complex number is real if and only if it equals its own conjugate.

Conjugation distributes over the basic complex arithmetic operations:

${\displaystyle {\overline {z\pm w}}={\overline {z}}\pm {\overline {w}},}$

${\displaystyle {\overline {z\cdot w}}={\overline {z}}\cdot {\overline {w}},\quad {\overline {z/w}}={\overline {z}}/{\overline {w}}.}$

Conjugation is also employed in inversive geometry, a branch of geometry studying reflections more general than ones about a line. In the network analysis of electrical circuits, the complex conjugate is used in finding the equivalent impedance when the maximum power transfer theorem is looked for.

Addition and subtractionEdit

Addition of two complex numbers can be done geometrically by constructing a parallelogram.

Two complex numbers ${\displaystyle a}$ and ${\displaystyle b}$ are most easily added by separately adding their real and imaginary parts of the summands. That is to say:

${\displaystyle a+b=(x+yi)+(u+vi)=(x+u)+(y+v)i.}$

Similarly, subtraction can be performed as

${\displaystyle a-b=(x+yi)-(u+vi)=(x-u)+(y-v)i.}$

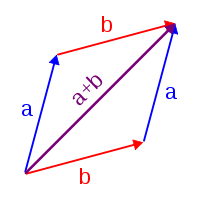
Using the visualization of complex numbers in the complex plane, the addition has the following geometric interpretation: the sum of two complex numbers ${\displaystyle a}$ and ${\displaystyle b}$, interpreted as points in the complex plane, is the point obtained by building a parallelogram from the three vertices ${\displaystyle O}$, and the points of the arrows labeled ${\displaystyle a}$ and ${\displaystyle b}$ (provided that they are not on a line). Equivalently, calling these points ${\displaystyle A,\;B,}$ respectively and the fourth point of the parallelogram ${\displaystyle X,}$ the triangles ${\displaystyle OAB}$ and ${\displaystyle XBA}$ are congruent. A visualization of the subtraction can be achieved by considering addition of the negative subtrahend.

MultiplicationEdit

Since the real part, the imaginary part, and the indeterminate ${\displaystyle i}$ in a complex number are all considered as numbers in themselves, two complex numbers, given as ${\displaystyle z=x+yi}$ and ${\displaystyle w=u+vi}$ are multiplied under the rules of the distributive property, the commutative properties and the defining property ${\displaystyle i^{2}=-1}$in the following way

${\displaystyle {\begin{aligned}z\cdot w&=(x+yi)\cdot (u+vi)&\\&=x(u+vi)+yi(u+vi)&&{\text{by the (right) distributive law}}\\&=xu+xvi+yiu+yivi&&{\text{by the (left) distributive law}}\\&=xu+yivi+xvi+yiu&&{\text{by the commutativity of addition}}\\&=xu+yvi^{2}+xvi+yui&&{\text{by the commutativity of multiplication}}\\&=(xu+yvi^{2})+(xvi+yui)&&{\text{by the associativity of addition}}\\&=(xu-yv)+(xvi+yui)&&{\text{by the defining property of }}i\\&=(xu-yv)+(xv+yu)i&&{\text{by the distributive law}}.\end{aligned}}}$

Reciprocal and divisionEdit

Using the conjugation, the reciprocal of a nonzero complex number z = x + yi can always be broken down to

${\displaystyle {\frac {1}{z}}={\frac {\overline {z}}{z{\overline {z}}}}={\frac {\overline {z}}{|z|^{2}}}={\frac {\overline {z}}{x^{2}+y^{2}}}={\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i,}$

since non-zero implies that ${\displaystyle x^{2}+y^{2}}$ is greater than zero.

This can be used to express a division of an arbitrary complex number ${\displaystyle w=u+vi}$ by a non-zero complex number ${\displaystyle z}$ as

${\displaystyle {\frac {w}{z}}=w\cdot {\frac {1}{z}}=(u+vi)\cdot \left({\frac {x}{x^{2}+y^{2}}}-{\frac {y}{x^{2}+y^{2}}}i\right)={\frac {1}{x^{2}+y^{2}}}\left((ux+vy)+(vx-uy)i\right).}$

Multiplication and division in polar formEdit

Multiplication of 2 + i (blue triangle) and 3 + i (red triangle). The red triangle is rotated to match the vertex of the blue one and stretched by √5, the length of the hypotenuse of the blue triangle.

Formulas for multiplication, division and exponentiation are simpler in polar form than the corresponding formulas in Cartesian coordinates. Given two complex numbers z₁ = r₁(cos φ₁ + i sin φ₁) and z₂ = r₂(cos φ₂ + i sin φ₂), because of the trigonometric identities

${\displaystyle \cos(a)\cos(b)-\sin(a)\sin(b)=\cos(a+b)}$

${\displaystyle \cos(a)\sin(b)+\sin(a)\cos(b)=\sin(a+b)}$

We may write,

${\displaystyle z_{1}z_{2}=r_{1}r_{2}(\cos(\varphi _{1}+\varphi _{2})+i\sin(\varphi _{1}+\varphi _{2})).}$

In other words, the absolute values are multiplied and the arguments are added to yield the polar form of the product. For example, multiplying by i corresponds to a quarter-turn counter-clockwise, which gives back i² = −1. The picture at the right illustrates the multiplication of

${\displaystyle (2+i)(3+i)=5+5i.}$

Since the real and imaginary part of 5 + 5i are equal, the argument of that number is 45 degrees, or π/4 (in radian). On the other hand, it is also the sum of the angles at the origin of the red and blue triangles are arctan(1/3) and arctan(1/2), respectively. Thus, the formula

${\displaystyle {\frac {\pi }{4}}=\arctan \left({\frac {1}{2}}\right)+\arctan \left({\frac {1}{3}}\right)}$

holds. As the arctan function can be approximated highly efficiently, formulas like this – known as Machin-like formulas – are used for high-precision approximations of π.

Similarly, division is given by

${\displaystyle {\frac {z_{1}}{z_{2}}}={\frac {r_{1}}{r_{2}}}\left(\cos(\varphi _{1}-\varphi _{2})+i\sin(\varphi _{1}-\varphi _{2})\right).}$

Square root

Edit

See also: Square roots of negative and complex numbers

The square roots of a + bi (with b ≠ 0) are ${\displaystyle \pm (\gamma +\delta i)}$, where

${\displaystyle \gamma ={\sqrt {\frac {a+{\sqrt {a^{2}+b^{2}}}}{2}}}}$

and

${\displaystyle \delta =\operatorname {sgn}(b){\sqrt {\frac {-a+{\sqrt {a^{2}+b^{2}}}}{2}}},}$

where sgn is the signum function. This can be seen by squaring ${\displaystyle \pm (\gamma +\delta i)}$ to obtain a + bi.^[25][26] Here ${\displaystyle {\sqrt {a^{2}+b^{2}}}}$ is called the modulus of a + bi, and the square root sign indicates the square root with non-negative real part, called the principal square root; also ${\displaystyle {\sqrt {a^{2}+b^{2}}}={\sqrt {z{\overline {z}}}},}$ where ${\displaystyle z=a+bi.}$^[27]

Functional equation

Edit

The exponential function satisfies the functional equation ${\displaystyle e^{z+t}=e^{z}e^{t}.}$ This can be proved either by comparing the power series expansion of both members or by applying analytic continuation from the restriction of the equation to real arguments.

Euler's formula

Edit

Euler's formula states that, for any real number x,

${\displaystyle e^{ix}=\cos x+i\sin x.}$

The functional equation implies thus that, if xand y are real, one has

${\displaystyle e^{x+iy}=e^{x}\cos y+ie^{x}\sin y,}$

which is the decomposition of the exponential function into its real and imaginary parts.

Complex logarithm

Edit

In the real case, the natural logarithm can be defined as the inverse of the exponential function. For extending this to the complex domain, one can start from Euler's formula. It implies that, if a complex number z is written in polar form

${\displaystyle z=r(\cos \varphi +i\sin \varphi ),}$

then its complex logarithm should be

${\displaystyle \ln(z)=\ln(r)+\varphi i.}$

However, because cosine and sine are periodic functions, the addition to ${\displaystyle \varphi }$ of an integer multiple of 2π. does not change z. For example, ${\displaystyle e^{i\pi }=e^{3i\pi }=-1}$, so both ${\displaystyle i\pi }$ and ${\displaystyle 3i\pi }$ are possible values for the natural logarithm of ${\displaystyle -1}$.

Therefore the complex logarithm must be defined as a multivalued function:

${\displaystyle \ln(z)=\left\{\ln(r)+\varphi i+2\pi ki\mid k\in \mathbb {Z} \right\}.}$

Alternatively, a branch cut can be used to define a true function. If z is not a negative real number, the principal value of the complex logarithm is obtained with ${\displaystyle -\pi <\varphi <\pi .}$ This is an analytic functionoutside the negative real numbers, but it cannot be prolongated to a function that is continuous at any negative real number.

It follows that if z is as above, and if t is another complex number, then the exponentiation is the multivalued function

${\displaystyle z^{t}=\left\{e^{t\ln r}\,(\cos(\varphi t+2\pi kt)+i\sin(\varphi t+2\pi kt))\}\mid k\in \mathbb {Z} \right\}}$

First learn about NUMBERS:

Types of NUMBERS; 

• Natural numbers
• Whole numbers
• Integers
• Rational numbers
• Irrational numbers
• Real numbers
• Algebraic numbers
• Complex numbers
• Imaginary numbers

The numbers used for counting. That is, the numbers 1, 2, 3, 4, etc.
Natural Numbers
Counting Numbers

Whole Numbers
Nonnegative Integers

The numbers 0, 1, 2, 3, 4, 5, etc.

 Integers

All positive and negative whole numbers (including zero). That is, the set {... , –3, –2, –1, 0, 1, 2, 3, ...}. Integers are indicated by either  or J.

Rational Numbers

All positive and negative fractions, including integers and so-called improper fractions. Formally, rational numbers are the set of all real numbers that can be written as a ratio of integers with nonzero denominator. Rational numbers are indicated by the symbol .

Note: Real numbers that aren't rational are called irrational.

Real Numbers All numbers on the number line. This includes (but is not limited to) positives and negatives, integers and rational numbers, square roots, cube roots , π (pi), etc. Real numbers are indicated by either  or .  Algebraic Numbers Real numbers that can occur as roots of polynomial equationsthat have integer coefficients. For example, all rational numbersare algebraic. So are all surds such as $\sqrt{7}$, as well as numbers built from surds such as the number below. $$\frac{42+\sqrt[3]{315.2}}{\sqrt{4-\sqrt{3}}}$$. Note: Real numbers which are not algebraic are known as transcendental numbers. Algebraic Numbers Real numbers that can occur as roots of polynomial equationsthat have integer coefficients. For example, all rational numbersare algebraic. So are all surds such as $\sqrt{7}$, as well as numbers built from surds such as the number below. $$\frac{42+\sqrt[3]{315.2}}{\sqrt{4-\sqrt{3}}}$$. Note: Real numbers which are not algebraic are known as transcendental numbers. Algebraic Numbers Real numbers that can occur as roots of polynomial equationsthat have integer coefficients. For example, all rational numbersare algebraic. So are all surds such as $\sqrt{7}$, as well as numbers built from surds such as the number below. $$\frac{42+\sqrt[3]{315.2}}{\sqrt{4-\sqrt{3}}}$$. Note: Real numbers which are not algebraic are known as transcendental numbers. Complex Numbers Numbers like 3 – 2i or  that can be written as the sum or difference of a real number and an imaginary number. Complex numbers are indicated by the symbol . Note: All real numbers and all pure imaginary numbers are complex. Sometimes, however, mathematicians use the phrase complex numbers to refer strictly to numbers which have both nonzero real parts and nonzero imaginary parts.

Complex Number Formulas

Algebra rules and formulas for complex numbers are listed below.

ImaginaryNumbers

Pure Imaginary Numbers

Complex numbers with no real part, such as 5i.

Real Numbers

All numbers on the number line. This includes (but is not limited to) positives and negatives, integers and rational numbers, square roots, cube roots , π (pi), etc. Real numbers are indicated by either  or .

Complex Conjugate

The complex conjugate of a + bi  is a – bi, and similarly the complex conjugate of a – bi  is a + bi. This consists of changing the sign of the imaginary part of a complex number. The real part is left unchanged.

Complex conjugates are indicated using a horizontal line over the number or variable. For example, .

Note: Complex conjugates are similar to, but not the same as, conjugates.

Expression	Complex Conjugate
5 – 2i 4i + 1 –5i 12	5 + 2i –4i + 1 5i 12

De Moivre’s Theorem

A formula useful for finding powers and roots of complex numbers.

Polar Form of a Complex Number

The polar coordinates of a complex number on the complex plane. The polar form of a complex number is written in any of the following forms: rcos θ + irsin θ, r(cos θ + isin θ), or rcis θ. In any of these forms r is called the modulus or absolute value. θ is called the argument.